PROBABILITÉS POKER
- Texas Hold'em Poker
Probabilités du Texas Hold'em Poker - Omaha Poker
Probabilités du Omaha Poker - Poker 5 Cartes
Probabilités du Poker à 5 cartes
CALCULATRICE POKER
- Calculatrice Poker
Calculateurs de cotes au poker
Probabilités au Texas Hold'em Poker
Lorsqu'on calcule les probabilités pour un jeu de cartes comme le Texas Hold'em, il y a deux approches de base. La première approche consiste à déterminer le nombre de résultats qui satisfont la condition en cours d'évaluation et de diviser ce nombre par le nombre total de résultats possibles.
Par exemple, il y a six résultats possibles pour tirer une paire d'as au Hold' em: {A♣, A♥}, {A♠, A♦}, {A♠, A♣}, {A♥, A♦}, {A♥, A♠}, and {A♦, A♣}. Il y a 52 façons de choisir la première carte et 51 façons de choisir la deuxième carte, et deux façons d'obtenir les deux cartes (52×51)/2=1326 résultats possibles sur les deux cartes distribués à un joueur. Cela donne une probabilité de tirer 2 as de .
La deuxième approche consiste à utiliser les probabilités conditionnelles, ou dans des situations plus complexes, un arbre de décision. Il ya 4 façons de tirer un As sur 52 choix pour la première carte résultant en une probabilité de Il existe 3 façons d'obtenir un As sur 51 choix sur la deuxième carte après avoir tiré un As sur la première carte soit une probabilité de
La probabilité conditionnelle de tirer deux As est le produit des deux probabilités:
Souvent, la clé pour déterminer la probabilité est de choisir la meilleure approche pour un problème donné.
Mains de départ
Au Texas Hold'em, un joueur reçoit deux cartes fermées. La première carte peut être l'une des 52 cartes dans le jeu et la deuxième carte peut être l'une des 51 cartes restantes. Cela donne 52 × 51 ÷ 2 = 1326 combinaisons possibles de main de départ (car l'ordre des cartes n'est pas significatif, les 2652 permutations sont divisées par les 2 ordres possibles des deux cartes). Sinon, le nombre de mains de départ possible est représentée comme le coefficient binomial
qui est le nombre de combinaisons possibles de choisir 2 cartes dans un jeu de 52 cartes à jouer.
Les 1326 mains de départ peut être réduite afin de déterminer la probabilité de mains de départ pour le Hold'em. Les seuls facteurs déterminant la force d'une main de départ sont les rangs de la carte et si les cartes partagent la même couleur. Sur les 1.326 combinaisons, il y a 169 mains de départ distinctes regroupées en trois formes: 13 paires de poche ou paire servie), 13 × 12 ÷ 2 = 78 mains assorties et 78 mains non assorties. La probabilité relative d'être une main de chaque forme donnée est différente. Le tableau suivant indique les chances et les probabilités au poker d'obtenir chaque type de main de départ.
-
Forme de main Nombre
de mainsCombinaisons
pour chaque mainCombinaisons Tirer une main spécifique Tirer n'importe quelle main Probabilité Cote Probabilité Cote Paire servie 13 13 × 6 = 78 220 : 1 16 : 1 Cartes assorties 78 78 × 4 = 312 331 : 1 3.25 : 1 Cartes non assorties 78 78 × 12 = 936 110 : 1 0.417 : 1
Voici les probabilités et les cotes pour obtenir divers autres types de mains de départ.
Main Probabilité Cote AKs (ou 2 cartes assorties spécifiques) 0.00302 331 : 1 AA (ou une paire spécifique) 0.00452 220 : 1 AKs, KQs, QJs, or JTs (cartes assorties) 0.0121 81.9 : 1 AK (2 cartes spécifiques, assorties ou non) 0.0121 81.9 : 1 AA, KK, ou QQ 0.0136 72.7 : 1 AA, KK, QQ ou JJ 0.0181 54.3 : 1 Cartes assorties , J ou mieux 0.0181 54.3 : 1 AA, KK, QQ, JJ, ou TT 0.0226 43.2 : 1 Cartes assorties, 10 ou mieux 0.0302 32.2 : 1 Connecteurs assorties 0.0392 24.5 : 1 Connecteurs, 10 ou mieux 0.0483 19.7 : 1 2 cartes supérieures ou égal à Q 0.0498 19.1 : 1 2 cartes supérieures ou égal à J 0.0905 10.1 : 1 2 cartes supérieures ou égal à T 0.143 5.98 : 1 Connecteurs (cartes se suivant) 0.157 5.38 : 1 2 cartes supérieures ou égal à 9 0.208 3.81 : 1 Non connectées, non assorties,
au moins une entre 2 et 90.534 0.873 : 1
Confrontation des mains de départ
Pour chaque main de départ donnée, il y a 50 × 49 ÷ 2 = 1,225 mains que l'adversaire peut avoir avant le flop (après le flop, le nombre de mains possibles que l'adversaire peut avoir est réduit par les 3 cartes révélées de communauté révélées au flop à 47 × 46 ÷ 2 = 1,081 mains). Par conséquent, il y a
confrontations possibles au Hold 'em (le nombre total de confrontations est divisé par les 2 possibilités de confrontation de 2 mains données). Par conséquent, puisqu'il y a seulement 169 mains de départ spécifiques, il y a 169 × 1,225 = 207,025 confrontations possibles en tête à tête.
Il est utile et intéressant de savoir comment deux mains de départ sont en concurrence les unes contre les autres avant le flop. En d'autres termes, nous supposons qu'aucune main ne soit couchée, et nous y irons jusqu'à l'abattage. Cette situation se produit assez souvent en No Limit en en tournoi. En outre, l'étude de ces cotes contribue à démontrer le concept de domination d'une main, ce qui est important dans tous les jeux de cartes de communauté.
Ce problème est bien plus compliqué que de déterminer la fréquence des mains distribuées. Pour comprendre pourquoi, compte tenu des deux mains distribuées, il y a 48 cartes restantes cachées. Sur ces 48 cartes, on peut choisir n'importe quelle combinaison de 5 cartes pour constituer le tableau (les 5 cartes de communauté). Ainsi, il ya
tableaux possibles qui peuvent arriver. En plus de déterminer avec précision le nombre de tableaux qui donnent une victoire à chaque joueur, nous devons aussi prendre en compte les tableaux qui partagent le pot, et répartir le nombre de ces tableaux entre les joueurs.
Le problème est trivial pour les ordinateurs qui peuvent le résoudre en recherche par force brute; il existe de nombreux logiciels disponibles qui calculent les cotes en très peu de temps. Un exercice un peu moins trivial est une analyse exhaustive de toutes les confrontations au Texas Hold 'em, qui exige l'évaluation de chaque tableau possible pour chaque confrontation distincte, ou 1.712.304 × 207 025 = 354 489 735 600 (≈ 354 000 000 000) résultats.
Confrontations des mains de départ en tête à tête
Quand on compare 2 mains de départ, la probabilité en tête à tête donne la chance qu'une main batte l'autre main après que toutes les cartes communes soient sorties. Les probabilités en tête à tête varient légèrement en fonction de chaque main de départ spécifique mais les probabilités moyennes sont listées dans le tableau suivant :
| Main joueur A | Probabilité A | Probabilité B | Main joueur B |
|---|---|---|---|
| Paire (Q-Q) |
0.83 | 0.17 | 2 cartes inférieures (9-6) |
| Paire supérieure (J-J) |
0.82 | 0.18 | Paire inférieure (8-8) |
| Paire supérieure (9-9) |
0.81 | 0.19 | Connecteurs inférieurs (5-6) |
| Paire supérieure (K-K) |
0.77 | 0.23 | Connecteurs assortis (4-5) |
| Kicker supérieur (K-9) |
0.71 | 0.29 | Kicker inférieur (K-7) |
| Paire (8-8) |
0.69 | 0.31 | 1 carte supérieure (J-7) |
| 2 cartes (K-9) |
0.68 | 0.32 | 2 cartes inférieures (8-5) |
| Paire (J-J) |
0.66 | 0.34 | Cartes assorties (K-8) |
| 1 carte supérieure (Q-9) |
0.64 | 0.36 | 1 carte intermédiaire (J-7) |
| 2 cartes (K-J) |
0.62 | 0.38 | Connecteurs inférieurs (10-9) |
| 2 cartes (J-10) |
0.58 | 0.42 | Connecteurs assortis inférieurs (9-8) |
| 1 carte supérieure (A-10) |
0.58 | 0.42 | 2 cartes intermédiaires (Q-J) |
| 1 carte supérieure (K-9) |
0.56 | 0.44 | Connecteurs (J-10) |
| Paire (6-6) |
0.55 | 0.45 | 2 cartes supérieures (Q-8) |
| 1 carte supérieure (A-3) |
0.52 | 0.48 | Connecteurs assortis (6-5) |
| Paire (9-9) |
0.50 | 0.50 | Connecteurs assortis supérieurs (K-Q) |
Starting hands against multiple opponents
When facing two opponents, for any given starting hand the number of possible combinations of hands the opponents can have is
hands. For calculating probabilities we can ignore the distinction between the two opponents holding A♠ J♥ and 8♥ 8♣ and the opponents holding 8♥ 8♣ and A♠ J♥. The number of ways that hands can be distributed between n opponents is n! (the factorial of n). So the number of unique hand combinations H against two opponents is
and against three opponents is
and against n opponents is
or alternatively
where (2n − 1)!! is the number of ways to distribute 2n cards between n hands of two cards each. The following table shows the number of hand combinations for up to nine opponents.
-
Opponents Number of possible hand combinations 1 1,225 2 690,900 3 238,360,500 4 56,372,258,250 5 ≈9.7073 × 1012 (more than 9 trillion) 6 ≈1.2620 × 1015 (more than 1 quadrillion) 7 ≈1.2674 × 1017 (more than 126 quadrillion) 8 ≈9.9804 × 1018 (almost 10 quintillion) 9 ≈6.2211 × 1020 (more than 622 quintillion)
An exhaustive analysis of all of the match ups in Texas Hold'em of a player against nine opponents requires evaluating each possible board for each distinct starting hand against each possible combination of hands held by nine opponents, which is
(more than 21 octillion).
Dominated hands
When evaluating a hand before the flop, it is useful to have some idea of how likely the hand is dominated. A dominated hand is a hand that is beaten by another hand (the dominant hand) and is extremely unlikely to win against it. Often the dominated hand has only a single card rank that can improve the dominated hand to beat the dominant hand (not counting straights and flushes). For example, KJ is dominated by KQ—both hands share the king, and the queen kicker is beating the jack kicker. Barring a straight or flush, the KJ will need a jack on the board to improve against the KQ (and would still be losing if a queen appears on the board along with the jack). A pocket pair is dominated by a pocket pair of higher rank.
Pocket pairs
Barring a straight or flush, a pocket pair needs to make three of a kind to beat a higher pocket pair. See the section "After the flop" for the odds of a pocket pair improving to three of a kind.
To calculate the probability that another player has a higher pocket pair, first consider the case against a single opponent. The probability that a single opponent has a higher pair can be stated as the probability that the first card dealt to the opponent is a higher rank than the pocket pair and the second card is the same rank as the first. Where r is the rank of the pocket pair (assigning values from 2–10 and J–A = 11–14), there are (14 − r) × 4 cards of higher rank. Subtracting the two cards for the pocket pair leaves 50 cards in the deck. After the first card is dealt to the player there are 49 cards left, 3 of which are the same rank as the first. So the probability P of a single opponent being dealt a higher pocket pair is
The following approach extends this equation to calculate the probability that one or more other players has a higher pocket pair.
- Multiply the base probability for a single player for a given rank of pocket pairs by the number of opponents in the hand;
- Subtract the adjusted probability that more than one opponent has a higher pocket pair. (This is necessary because this probability effectively gets added to the calculation multiple times when multiplying the single player result.
Where n is the number of other players still in the hand and Pma is the adjusted probability that multiple opponents have higher pocket pairs, then the probability that at least one of them has a higher pocket pair is
The calculation for Pma depends on the rank of the player's pocket pair, but can be generalized as
where P2 is the probability that exactly two players have a higher pair, P3 is the probability that exactly three players have a higher pair, etc. As a practical matter, even with pocket 2s against 9 opponents, P4 < 0.0015 and P5 < 0.00009, so just calculating P2 and P3 gives an adequately precise result.
The following table shows the probability that before the flop another player has a larger pocket pair when there are one to nine other players in the hand.
-
Probability of facing a
larger pair when holdingAgainst 1 Against 2 Against 3 Against 4 Against 5 Against 6 Against 7 Against 8 Against 9 KK 0.0049 0.0098 0.0147 0.0196 0.0244 0.0293 0.0342 0.0391 0.0439 QQ 0.0098 0.0195 0.0292 0.0388 0.0484 0.0579 0.0673 0.0766 0.0859 JJ 0.0147 0.0292 0.0436 0.0577 0.0717 0.0856 0.0992 0.1127 0.1259 TT 0.0196 0.0389 0.0578 0.0764 0.0946 0.1124 0.1299 0.1470 0.1637 99 0.0245 0.0484 0.0718 0.0946 0.1168 0.1384 0.1593 0.1795 0.1990 88 0.0294 0.0580 0.0857 0.1125 0.1384 0.1634 0.1873 0.2101 0.2318 77 0.0343 0.0674 0.0994 0.1301 0.1595 0.1874 0.2138 0.2387 0.2619 66 0.0392 0.0769 0.1130 0.1473 0.1799 0.2104 0.2389 0.2651 0.2890 55 0.0441 0.0862 0.1263 0.1642 0.1996 0.2324 0.2623 0.2892 0.3129 44 0.0490 0.0956 0.1395 0.1806 0.2186 0.2532 0.2841 0.3109 0.3334 33 0.0539 0.1048 0.1526 0.1967 0.2370 0.2729 0.3040 0.3300 0.3503 22 0.0588 0.1141 0.1654 0.2124 0.2546 0.2914 0.3222 0.3464 0.3633
The following table gives the probability that a hand is facing two or more larger pairs before the flop. From the previous equations, the probability Pm is computed as
-
Probability of facing multiple
larger pairs when holdingAgainst 2 Against 3 Against 4 Against 5 Against 6 Against 7 Against 8 Against 9 KK < 0.00001 0.00001 0.00003 0.00004 0.00007 0.00009 0.00012 0.00016 QQ 0.00006 0.00018 0.00037 0.00061 0.00091 0.00128 0.00171 0.00220 JJ 0.00017 0.00051 0.00102 0.00171 0.00257 0.00360 0.00482 0.00621 TT 0.00033 0.00099 0.00200 0.00335 0.00504 0.00709 0.00950 0.01226 99 0.00054 0.00164 0.00330 0.00553 0.00836 0.01177 0.01580 0.02045 88 0.00081 0.00244 0.00493 0.00828 0.01253 0.01769 0.02378 0.03084 77 0.00112 0.00341 0.00689 0.01160 0.01758 0.02487 0.03351 0.04353 66 0.00149 0.00454 0.00918 0.01550 0.02353 0.03335 0.04503 0.05861 55 0.00191 0.00583 0.01182 0.01998 0.03040 0.04318 0.05840 0.07619 44 0.00239 0.00728 0.01480 0.02506 0.03821 0.05438 0.07371 0.09635 33 0.00291 0.00890 0.01812 0.03075 0.04698 0.06699 0.09099 0.11919 22 0.00349 0.01068 0.02180 0.03706 0.05673 0.08107 0.11034 0.14484
From a practical perspective, however, the odds of out drawing a single pocket pair or multiple pocket pairs are not much different. In both cases the large majority of winning hands require one of the remaining two cards needed to make three of a kind. The real difference against multiple overpairs becomes the increased probability that one of the overpairs will also make three of a kind.
Hands with one ace
When holding a single ace (referred to as Ax), it is useful to know how likely it is that another player has a better ace—an ace with a higher second card. The weaker ace is dominated by the better ace. The probability that a single opponent has a better ace is the probability that he has either AA or Ax where x is a rank other than ace that is higher than the player's second card. When holding Ax, the probability that a chosen single player has AA is 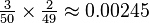 . In the case of a table with n opponents, the probability of one of them holding AA is (1 − (1 − 0.00245)n). If the player is holding Ax against 9 opponents, there is a probability of approximately 0.0218 that one opponent has AA.
. In the case of a table with n opponents, the probability of one of them holding AA is (1 − (1 − 0.00245)n). If the player is holding Ax against 9 opponents, there is a probability of approximately 0.0218 that one opponent has AA.
Where x is the rank 2–K of the second card (assigning values from 2–10 and J–K = 11–13) the probability that a single opponent has a better ace is calculated by the formula
The probability of a player having Ay, where y is a rank such that x < y <= K, is multiplied by the two ways to order the cards A and y in the hand.
The following table shows the probability that before the flop another player has an ace with a larger kicker in the hand.
-
Probability of facing an ace
with larger kicker when holdingAgainst 1 Against 2 Against 3 Against 4 Against 5 Against 6 Against 7 Against 8 Against 9 AK 0.00245 0.00489 0.00733 0.00976 0.01219 0.01460 0.01702 0.01942 0.02183 AQ 0.01224 0.02434 0.03629 0.04809 0.05974 0.07126 0.08263 0.09386 0.10496 AJ 0.02204 0.04360 0.06468 0.08529 0.10545 0.12517 0.14445 0.16331 0.18175 AT 0.03184 0.06266 0.09250 0.12139 0.14937 0.17645 0.20267 0.22805 0.25263 A9 0.04163 0.08153 0.11977 0.15642 0.19154 0.22520 0.25745 0.28837 0.31799 A8 0.05143 0.10021 0.14649 0.19038 0.23202 0.27152 0.30898 0.34452 0.37823 A7 0.06122 0.11870 0.17266 0.22331 0.27086 0.31550 0.35741 0.39675 0.43369 A6 0.07102 0.13700 0.19829 0.25523 0.30812 0.35726 0.40291 0.44531 0.48471 A5 0.08082 0.15510 0.22338 0.28615 0.34384 0.39687 0.44561 0.49041 0.53160 A4 0.09061 0.17301 0.24795 0.31609 0.37806 0.43442 0.48567 0.53227 0.57465 A3 0.10041 0.19073 0.27199 0.34509 0.41085 0.47000 0.52322 0.57109 0.61416 A2 0.11020 0.20826 0.29552 0.37315 0.44223 0.50370 0.55840 0.60706 0.65037
The flop
The value of a starting hand can change dramatically after the flop. Regardless of initial strength, any hand can flop the nuts—for example, if the flop comes with three 2s, any hand holding the fourth 2 has the nuts (though additional cards could still give another player a higher four of a kind or a straight flush). Conversely, the flop can undermine the perceived strength of any hand—a player holding A♣ A♥ would not be happy to see 8♠ 9♠ 10♠ on the flop because of the straight and flush possibilities.
There are
possible flops for any given starting hand. By the turn the total number of combinations has increased to
and on the river there are
possible boards to go with the hand.
The following are some general probabilities about what can occur on the board. These assume a "random" starting hand for the player.
-
Board consisting of Making on flop Making by turn Making by river Prob. Odds Prob. Odds Prob. Odds Three or more of same suit 0.05177 18.3 : 1 0.13522 6.40 : 1 0.23589 3.24 : 1 Four or more of same suit 0.01056 93.7 : 1 0.03394 28.5 : 1 Rainbow flop (all different suits) 0.39765 1.51 : 1 0.10550 8.48 : 1 Three cards of consecutive rank (but not four consecutive) 0.03475 27.8 : 1 0.11820 7.46 : 1 0.25068 2.99 : 1 Four cards to a straight (but not five) 0.03877 24.8 : 1 0.18991 4.27 : 1 Three or more cards of consecutive rank and same suit 0.00217 459 : 1 0.00869 114 : 1 0.02172 45.0 : 1 Three of a kind (but not a full house or four of a kind) 0.00235 424 : 1 0.00935 106 : 1 0.02128 46 : 1 A pair (but not two pair or three or four of a kind) 0.16941 4.90 : 1 0.30417 2.29 : 1 0.42450 1.36 : 1 Two pair (but not a full house) 0.01037 95.4 : 1 0.04716 20.2 : 1
An interesting fact to note from the table above is that more than 60% of the flops will have at least two of the same suit—you're likely to either be drawing to a flush or worried about one.
Flopping overcards when holding a pocket pair
It is also useful to look at the chances different starting hands have of either improving on the flop, or of weakening on the flop. One interesting circumstance concerns pocket pairs. When holding a pocket pair, overcards (cards of higher rank than the pair) weaken the hand because of the potential that an overcard has paired a card in an opponent's hand. The hand gets worse the more overcards there are on the board and the more opponents that are in the hand because the probability that one of the overcards has paired a hole card increases. To calculate the probability of no overcard, take the total number of outcomes without an overcard divided by the total number of outcomes.
Where x is the rank 3–K of the pocket pair (assigning values from 3–10 and J–K = 11–13), then the number of overcards is and the number of cards of rank x or less is
. The number of outcomes without an overcard is the number of combinations that can be formed with the remaining cards, so the probability P of an overcard on the flop is
and on the turn and river are
and
respectively.
The following table gives the probability that no overcards will come on the flop, turn and river, for each of the pocket pairs from 3 to K.
-
Holding pocket pair No overcard on flop No overcard by turn No overcard by river Prob. Odds Prob. Odds Prob. Odds KK 0.7745 0.29 : 1 0.7086 0.41 : 1 0.6470 0.55 : 1 QQ 0.5857 0.71 : 1 0.4860 1.06 : 1 0.4015 1.49 : 1 JJ 0.4304 1.32 : 1 0.3205 2.12 : 1 0.2369 3.22 : 1 TT 0.3053 2.28 : 1 0.2014 3.97 : 1 0.1313 6.61 : 1 99 0.2071 3.83 : 1 0.1190 7.40 : 1 0.0673 13.87 : 1 88 0.1327 6.54 : 1 0.0649 14.40 : 1 0.0310 31.21 : 1 77 0.0786 11.73 : 1 0.0318 30.48 : 1 0.0124 79.46 : 1 66 0.0416 23.02 : 1 0.0133 74.26 : 1 0.0040 246.29 : 1 55 0.0186 52.85 : 1 0.0043 229.07 : 1 0.0009 1,057.32 : 1 44 0.0061 162.33 : 1 0.0009 1,095.67 : 1 0.0001 8,406.78 : 1 33 0.0010 979.00 : 1 0.0001 15,352.33 : 1 0.0000 353,125.67 : 1
Notice that there is a better than 35% probability that an ace will come by the river if holding pocket kings, and with pocket queens, the odds are slightly in favor of an ace or a king coming by the turn, and a full 60% in favor of an overcard to the queen by the river. With pocket jacks, there's only a 43% chance that an overcard will not come on the flop and it is better than 3 : 1 that an overcard will come by the river.
Notice, though, that those probabilities would be lower if we consider that at least one opponent happens to hold one of those overcards.
After the flop - outs
During play—that is, from the flop and onwards—drawing probabilities come down to a question of outs. All situations which have the same number of outs have the same probability of improving to a winning hand over any unimproved hand held by an opponent. For example, an inside straight draw (e.g. 3-4-6-7 missing the 5 for a straight), and a full house draw (e.g. 6-6-K-K drawing for one of the pairs to become three-of-a-kind) are equivalent. Each can be satisfied by four cards—four 5s in the first case, and the other two 6s and other two kings in the second.
The probabilities of drawing these outs are easily calculated. At the flop there remain 47 unseen cards, so the probability is (outs ÷ 47). At the turn there are 46 unseen cards so the probability is (outs ÷ 46). The cumulative probability of making a hand on either the turn or river can be determined as the complement of the odds of not making the hand on the turn and not on the river. The probability of not drawing an out is (47 − outs) ÷ 47 on the turn and (46 − outs) ÷ 46 on the river; taking the complement of these conditional probabilities gives the probability of drawing the out by the river which is calculated by the formula
For reference, the probability and odds for some of the more common numbers of outs are given here.
-
Example drawing to Outs Make on turn Make on river Make on turn or river Prob. Odds Prob. Odds Prob. Odds Inside straight flush; Four of a kind 1 0.0213 46.0 : 1 0.0217 45.0 : 1 0.0426 22.5 : 1 Open-ended straight flush; Three of a kind 2 0.0426 22.5 : 1 0.0435 22.0 : 1 0.0842 10.9 : 1 High pair 3 0.0638 14.7 : 1 0.0652 14.3 : 1 0.1249 7.01 : 1 Inside straight; Full house 4 0.0851 10.7 : 1 0.0870 10.5 : 1 0.1647 5.07 : 1 Three of a kind or two pair 5 0.1064 8.40 : 1 0.1087 8.20 : 1 0.2035 3.91 : 1 Either pair 6 0.1277 6.83 : 1 0.1304 6.67 : 1 0.2414 3.14 : 1 Full house or four of a kind; (see note)
Inside straight or high pair7 0.1489 5.71 : 1 0.1522 5.57 : 1 0.2784 2.59 : 1 Open-ended straight 8 0.1702 4.88 : 1 0.1739 4.75 : 1 0.3145 2.18 : 1 Flush 9 0.1915 4.22 : 1 0.1957 4.11 : 1 0.3497 1.86 : 1 Inside straight or pair 10 0.2128 3.70 : 1 0.2174 3.60 : 1 0.3839 1.60 : 1 Open-ended straight or high pair 11 0.2340 3.27 : 1 0.2391 3.18 : 1 0.4172 1.40 : 1 Inside straight or flush; Flush or high pair 12 0.2553 2.92 : 1 0.2609 2.83 : 1 0.4496 1.22 : 1 13 0.2766 2.62 : 1 0.2826 2.54 : 1 0.4810 1.08 : 1 Open-ended straight or pair 14 0.2979 2.36 : 1 0.3043 2.29 : 1 0.5116 0.955 : 1 Open-ended straight or flush; Flush or pair;
Inside straight, flush or high pair15 0.3191 2.13 : 1 0.3261 2.07 : 1 0.5412 0.848 : 1 16 0.3404 1.94 : 1 0.3478 1.88 : 1 0.5698 0.755 : 1 17 0.3617 1.76 : 1 0.3696 1.71 : 1 0.5976 0.673 : 1 Inside straight or flush or pair;
Open-ended straight, flush or high pair18 0.3830 1.61 : 1 0.3913 1.56 : 1 0.6244 0.601 : 1 19 0.4043 1.47 : 1 0.4130 1.42 : 1 0.6503 0.538 : 1 20 0.4255 1.35 : 1 0.4348 1.30 : 1 0.6753 0.481 : 1 Open-ended straight, flush or pair 21 0.4468 1.24 : 1 0.4565 1.19 : 1 0.6994 0.430 : 1
- Note: When drawing to a full house or four of a kind with a pocket pair that has hit trips (three of a kind) on the flop, there are 6 outs to get a full house by pairing the board and one out to make four of a kind. This means that if the turn does not pair the board or make four of a kind, there will be 3 additional outs on the river, for a total of 10, to pair the turn card and make a full house. This makes the probability of drawing to a full house or four of a kind on the turn or river 0.334 and the odds are 1.99 : 1. This makes drawing to a full house or four of a kind by the river about 8½ outs.
If a player doesn't fold before the river, a hand with at least 14 outs after the flop has a better than 50% chance to catch one of its outs on either the turn or the river. With 20 or more outs, a hand is a better than 2 : 1 favorite to catch at least one out in the two remaining cards.
Estimating probability of drawing outs - The rule of four and two
Many poker players do not have the mathematical ability to calculate odds in the middle of a poker hand. One solution is to just memorize the odds of drawing outs at the river and turn since these odds are needed frequently for making decisions. Another solution some players use is an easily calculated approximation of the probability for drawing outs, commonly referred to as the "Rule of Four and Two". With two cards to come, the percent chance of hitting x outs is about (x × 4)%. This approximation gives roughly accurate probabilities up to about 12 outs after the flop, with an absolute average error of 0.9%, a maximum absolute error of 3%, a relative average error of 3.5% and a maximum relative error of 6.8%. With one card to come, the percent chance of hitting x is about (x × 2)%. This approximation has a constant relative error of an 8% underestimation, which produces a linearly increasing absolute error of about 1% for each 6 outs.
A slightly more complicated, but significantly more accurate approximation of drawing outs after the flop is to use (x × 4)% for up to 9 outs and (x × 3 + 9)% for 10 or more outs. This approximation has a maximum absolute error of less than 1% for 1 to 19 outs and maximum relative error of less than 5% for 2 to 23 outs. A more accurate approximation for the probability of drawing outs after the turn is (x × 2 + (x × 2) ÷ 10)%. This is easily done by first multiplying x by 2, then rounding the result to the nearest multiple of ten and adding the 10's digit to the first result. For example, 12 outs would be 12 × 2 = 24, 24 rounds to 20, so the approximation is 24 + 2 = 26%. This approximation has a maximum absolute error of less than 0.9% for 1 to 19 outs and a maximum relative error of 3.5% for more than 3 outs. The following shows the approximations and their absolute and relative errors for both methods of approximation.
-
Outs Make on turn or river Make on river Actual (x × 4)% (x × 3 + 9)% Actual (x × 2)% (x × 2 + (x × 2) ÷ 10)% Est. Error % Error Est. Error % Error Est. Error % Error Est. Error % Error 1 4.2553% 4% −0.26% 6.00% 4% −0.26% 6.00% 2.1739% 2% −0.17% 8.00% 2% −0.17% 8.00% 2 8.4181% 8% −0.42% 4.97% 8% −0.42% 4.97% 4.3478% 4% −0.35% 8.00% 4% −0.35% 8.00% 3 12.4884% 12% −0.49% 3.91% 12% −0.49% 3.91% 6.5217% 6% −0.52% 8.00% 7% +0.48% 7.33% 4 16.4662% 16% −0.47% 2.83% 16% −0.47% 2.83% 8.6957% 8% −0.70% 8.00% 9% +0.30% 3.50% 5 20.3515% 20% −0.35% 1.73% 20% −0.35% 1.73% 10.8696% 10% −0.87% 8.00% 11% +0.13% 1.20% 6 24.1443% 24% −0.14% 0.60% 24% −0.14% 0.60% 13.0435% 12% −1.04% 8.00% 13% −0.04% 0.33% 7 27.8446% 28% +0.16% 0.56% 28% +0.16% 0.56% 15.2174% 14% −1.22% 8.00% 15% −0.22% 1.43% 8 31.4524% 32% +0.55% 1.74% 32% +0.55% 1.74% 17.3913% 16% −1.39% 8.00% 18% +0.61% 3.50% 9 34.9676% 36% +1.03% 2.95% 36% +1.03% 2.95% 19.5652% 18% −1.57% 8.00% 20% +0.43% 2.22% 10 38.3904% 40% +1.61% 4.19% 39% +0.61% 1.59% 21.7391% 20% −1.74% 8.00% 22% +0.26% 1.20% 11 41.7206% 44% +2.28% 5.46% 42% +0.28% 0.67% 23.9130% 22% −1.91% 8.00% 24% +0.09% 0.36% 12 44.9584% 48% +3.04% 6.77% 45% +0.04% 0.09% 26.0870% 24% −2.09% 8.00% 26% −0.09% 0.33% 13 48.1036% 52% +3.90% 8.10% 48% −0.10% 0.22% 28.2609% 26% −2.26% 8.00% 29% +0.74% 2.62% 14 51.1563% 56% +4.84% 9.47% 51% −0.16% 0.31% 30.4348% 28% −2.43% 8.00% 31% +0.57% 1.86% 15 54.1166% 60% +5.88% 10.87% 54% −0.12% 0.22% 32.6087% 30% −2.61% 8.00% 33% +0.39% 1.20% 16 56.9843% 64% +7.02% 12.31% 57% +0.02% 0.03% 34.7826% 32% −2.78% 8.00% 35% +0.22% 0.62% 17 59.7595% 68% +8.24% 13.79% 60% +0.24% 0.40% 36.9565% 34% −2.96% 8.00% 37% +0.04% 0.12% 18 62.4422% 72% +9.56% 15.31% 63% +0.56% 0.89% 39.1304% 36% −3.13% 8.00% 40% +0.87% 2.22% 19 65.0324% 76% +10.97% 16.86% 66% +0.97% 1.49% 41.3043% 38% −3.30% 8.00% 42% +0.70% 1.68% 20 67.5301% 80% +12.47% 18.47% 69% +1.47% 2.18% 43.4783% 40% −3.48% 8.00% 44% +0.52% 1.20% 21 69.9352% 84% +14.06% 20.11% 72% +2.06% 2.95% 45.6522% 42% −3.65% 8.00% 46% +0.35% 0.76% 22 72.2479% 88% +15.75% 21.80% 75% +2.75% 3.81% 47.8261% 44% −3.83% 8.00% 48% +0.17% 0.36% 23 74.4681% 92% +17.53% 23.54% 78% +3.53% 4.74% 50.0000% 46% −4.00% 8.00% 51% +1.00% 2.00%
Either of these approximations is generally accurate enough to aid in most pot odds calculations.
Runner-runner outs
Some outs for a hand require drawing an out on both the turn and the river—making two consecutive outs is called a runner-runner. Examples would be needing two cards to make a straight, flush, or three or four of a kind. Runner-runner outs can either draw from a common set of outs or from disjoint sets of outs. Two disjoint outs can either be conditional or independent events.
Common outs
Drawing to a flush is an example of drawing from a common set of outs. Both the turn and river need to be the same suit, so both outs are coming from a common set of outs—the set of remaining cards of the desired suit. After the flop, if x is the number of common outs, the probability P of drawing runner-runner outs is
Since a flush would have 10 outs, the probability of a runner-runner flush draw is . Other examples of runner-runner draws from a common set of outs are drawing to three or four of a kind. When counting outs, it is convenient to convert runner-runner outs to "normal" outs (see "After the flop"). A runner-runner flush draw is about the equivalent of one "normal" out.
The following table shows the probability and odds of making a runner-runner from a common set of outs and the equivalent normal outs.
-
Likely drawing to Common outs Probability Odds Equivalent outs Four of a kind (with pair)
Inside-only straight flush2 0.00093 1,080 : 1 0.02 Three of a kind (with no pair) 3 0.00278 359 : 1 0.07 4 0.00556 179 : 1 0.13 5 0.00925 107 : 1 0.22 Two pair or three of a kind (with no pair) 6 0.01388 71.1 : 1 0.33 7 0.01943 50.5 : 1 0.46 8 0.02590 37.6 : 1 0.61 9 0.03330 29.0 : 1 0.78 Flush 10 0.04163 23.0 : 1 0.98
Disjoint outs
Two outs are disjoint when there are no common cards between the set of cards needed for the first out and the set of cards needed for the second out. The outs are independent of each other if it does not matter which card comes first, and one card appearing does not affect the probability of the other card appearing except by changing the number of remaining cards; an example is drawing two cards to an inside straight. The outs are conditional on each other if the number of outs available for the second card depends on the first card; an example is drawing two cards to an outside straight.
After the flop, if x is the number of independent outs for one card and y is the number of outs for the second card, then the probability P of making the runner-runner is
For example, a player holding J♦ Q♦ after the flop 9♥ 5♣ 4♠ needs a 10 and either a K or 8 on the turn and river to make a straight. There are 4 10s and 8 kings and 8s, so the probability is .
The probability of making a conditional runner-runner depends on the condition. For example, a player holding 9♥ 10♥ after the flop 8♦ 2♠ A♣ can make a straight with {J, Q}, {7, J} or {6, 7}. The number of outs for the second card is conditional on the first card—a Q or 6 (8 cards) on the first card leaves only 4 outs (J or 7, respectively) for the second card, while a J or 7 (8 cards) for the first card leaves 8 outs ({Q, 7} or {J, 6}, respectively) for the second card. The probability P of a runner-runner straight for this hand is calculated by the equation
The following table shows the probability and odds of making a runner-runner from a disjoint set of outs for common situations and the equivalent normal outs.
-
Drawing to Probability Odds Equivalent outs Outside straight 0.04440 21.5 : 1 1.04 Inside+outside straight 0.02960 32.8 : 1 0.70 Inside-only straight 0.01480 66.6 : 1 0.35 Outside straight flush 0.00278 359 : 1 0.07 Inside+outside straight flush 0.00185 540 : 1 0.04
The preceding table assumes the following definitions.
- Outside straight and straight flush
- Drawing to a sequence of three cards of consecutive rank from 3-4-5 to 10-J-Q where two cards can be added to either end of the sequence to make a straight or straight flush.
- Inside+outside straight and straight flush
- Drawing to a straight or straight flush where one required rank can be combined with one of two other ranks to make the hand. This includes sequences like 5-7-8 which requires a 6 plus either a 4 or 9 as well as the sequences J-Q-K, which requires a 10 plus either a 9 or A, and 2-3-4 which requires a 5 plus either an A or 6.
- Inside-only straight and straight flush
- Drawing to a straight or straight flush where there are only two ranks that make the hand. This includes hands such as 5-7-9 which requires a 6 and an 8 as well as A-2-3 which requires a 4 and a 5.
Compound outs
The strongest runner-runner probabilities lie with hands that are drawing to multiple hands with different runner-runner combinations. These include hands that can make a straight, flush or straight flush, as well as four of a kind or a full house. Calculating these probabilities requires adding the compound probabilities for the various outs, taking care to account for any shared hands. For example, if Ps is the probability of a runner-runner straight, Pf is the probability of a runner-runner flush, and Psf is the probability of a runner-runner straight flush, then the compound probability P of getting one of these hands is
- P = Ps + Pf − Psf.
The probability of the straight flush is subtracted from the total because it is already included in both the probability of a straight and the probability of a flush, so it has been added twice and must therefore be subtracted from the compound outs of a straight or flush.
The following table gives the compound probability and odds of making a runner-runner for common situations and the equivalent normal outs.
-
Drawing to Probability Odds Equivalent outs Flush, outside straight or straight flush 0.08326 11.0 : 1 1.98 Flush, inside+outside straight or straight flush 0.06938 13.4 : 1 1.65 Flush, inside-only straight or straight flush 0.05550 17.0 : 1 1.30
Some hands have even more runner-runner chances to improve. For example, holding the hand J♠ Q♠ after a flop of 10♠ J♥ 7♦ there are several runner-runner hands to make at least a straight. The hand can get two cards from the common outs of {J, Q} (5 cards) to make a full house or four of a kind, can get a J (2 cards) plus either a 7 or 10 (6 cards) to make a full house from these independent disjoint outs, and is drawing to the compound outs of a flush, outside straight or straight flush. The hand can also make {7, 7} or {10, 10} (each drawing from 3 common outs) to make a full house, although this will make four of a kind for anyone holding the remaining 7 or 10 or a bigger full house for anyone holding an overpair. Working from the probabilities from the previous tables and equations, the probability P of making one of these runner-runner hands is a compound probability
and odds of 8.16 : 1 for the equivalent of 2.59 normal outs. Almost all of these runner-runners give a winning hand against an opponent who had flopped a straight holding 8, 9, but only some give a winning hand against A♠ 2♠ (this hand makes bigger flushes when a flush is hit) or against K♣ Q♦ (this hand makes bigger straights when a straight is hit with 8 9). When counting outs, it is necessary to adjust for which outs are likely to give a winning hand—this is where the skill in poker becomes more important than being able to calculate the probabilities.
Home > Probabilités Texas Hold'em Poker


